슈바르츠실트 계량

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

슈바르츠실트 계량은 전하와 자하가 0인 정적이고 구면 대칭을 가지며, 회전하거나 대전되지 않은 구형 별을 나타내는 시공간의 계량이다. 이는 블랙홀의 질량, 각운동량, 전하, 자하만으로 결정된다는 털없음 정리에 따라, 전하와 자하가 0인 블랙홀을 나타내는 해이기도 하다. 슈바르츠실트 계량은 아인슈타인 방정식의 해이며, 슈바르츠실트 좌표를 사용해 표현된다. 이 계량은 질량이 큰 물체 주위의 중력장을 묘사하며, 지구와 태양과 같은 천체에 적용될 수 있다. 슈바르츠실트 해는 $r=0$과 $r=r_s$에서 특이점을 가지며, $r=r_s$는 사건 지평선으로 블랙홀의 경계를 나타낸다. 이 해는 다양한 좌표계로 표현될 수 있으며, 궤도 운동과 관련된 특징을 보여준다. 슈바르츠실트 해는 1916년 카를 슈바르츠실트에 의해 처음 발표되었으며, 일반 상대성 이론의 중요한 해 중 하나로 여겨진다.

2. 정의

털없음 정리에 따라, 블랙홀은 질량, 각운동량, 전하, 자하만으로 결정된다. '''슈바르츠실트 계량'''은 전하·자하가 0인 정적인, 점근적으로 민코프스키 공간에 존재하는 유일한 구면 대칭 해이며, 회전하거나 대전되어 있지 않는 구형 별을 나타낸다. 만약 별의 크기가 슈바르츠실트 계량보다 작다면 블랙홀이 된다.

광속을 $c=1$ 로 놓고, −+++… 계량 부호수를 사용하면 $d>3$ 차원 시공간에서 '''슈바르츠실트 계량'''은

: $\mathrm ds^2=-\left(1-(r_0/r)^{d-3}\right)\mathrm dt^2+\left(1-(r_0/r)^{d-3}\right)^{-1}\mathrm dr^2+r^2\,\mathrm d\Omega^2_{d-2}$

이 된다.^[47]

여기서,

$r_0$ 는 길이의 단위를 가지는, 사건 지평선의 위치를 나타내는 임의의 매개 변수이다.
$d\Omega_{d-2}^2$ 는 반지름이 1인 $d-2$ 차원 초구 $S^{d-2}$ 의 부피 원소로, 예를 들어 4차원 $d=4$ 인 경우, 이는 다음과 같은 구면 좌표계 넓이의 원소이다.

:

\mathrm d\Omega^2 = \mathrm d\theta^2 + \sin^2 \theta\mathrm d\phi^2

3차원 이하에서는 이와 같은 사건의 지평선을 갖는 슈바르츠실트 해가 존재하지 않는다. (다만 음의 우주 상수의 경우 BTZ 블랙홀이라는 해가 존재한다.)

슈바르츠실트 계량은 구면 대칭 로렌츠 계량으로, 빈 공간에서 아인슈타인의 장 방정식의 해이다. 이는 중력체를 제외한 ''바깥''에서만 유효하며, 반지름

R

인 구형 물체의 경우

r > R

에서 유효하다. 중력체 내부와 외부 모두를 설명하기 위해 슈바르츠실트 해는

r = R

에서 내부 슈바르츠실트 계량과 같은 적절한 내부 해와 일치해야 한다.^[4]

슈바르츠실트 좌표

(t, r, \theta, \phi)

에서 슈바르츠실트 계량 (또는 그에 상응하는, 고유 시간에 대한 선 요소)은 다음과 같다.

:

{d s}^{2} = c^2 \,{d \tau}^{2} = \left (1 - \frac{r_\mathrm{s}}{r} \right) c^2 \,dt^2 - \left(1-\frac{r_\mathrm{s}}{r}\right)^{-1} \,dr^2 - r^2 {d \Omega}^{2},

여기서

{d \Omega}^{2} = \left(d\theta^2 + \sin^2\theta \, d\phi^2\right)

는 2차원 구에 대한 계량이다. 또한,

$d\tau^2$ 는 시간 유사 곡선에 대해 양수이며, 이 경우 $\tau$ 는 고유 시간이다 (같은 세계선을 따라 움직이는 시계로 측정한 시간으로, 시험 입자와 동일).
$c$ 는 광속이다.
$t$ 는 $r > r_\text{s}$ 에 대해 질량이 큰 물체로부터 무한히 멀리 떨어져 있고 이에 대해 정지해 있는 시계로 측정된 시간 좌표이다.
$r$ 는 $r > r_\text{s}$ 에 대해 질량이 큰 물체 주위에 중심이 있는 구의 둘레를 2π로 나눈 값으로 측정된 반경 좌표이다.
$\Omega$ 는 2차원 구 $S^2$ 의 한 점이다.
$\theta$ 는 임의로 "z"축을 선택한 후 정의되는 $\Omega$ 의 위도이다 (북쪽으로부터의 각도, 라디안 단위)
$\phi$ 는 선택된 "z"축 주위의 $\Omega$ 의 경도이다 (또한 라디안 단위)
$r_\text{s}$ 는 질량이 큰 물체의 슈바르츠실트 반지름이며, 질량 $M$ 과 $r_\text{s} = {2GM}/{c^2}$ 로 관련된 척도 인자이며, 여기서 $G$ 는 중력 상수이다.^[5]

반경 좌표는 "방사형으로 움직이는 측지선 시계에 대해 동시에 발생하는 두 사건 사이의 고유 거리, 두 사건이 동일한 방사형 좌표선에 놓여 있음"으로 물리적 중요성을 갖는다.^[7]

슈바르츠실트 해는 점 입자 주위의 중력장에 해당하는 고전적인 뉴턴 중력 이론과 유사하며, 지구 표면에서도 뉴턴 중력에 대한 수정은 10억 분의 1에 불과하다.^[8] 지구의 슈바르츠실트 반지름은 약 8.9mm이고,^[6] 태양의 슈바르츠실트 반지름은 약 3.0km이다. 이 비율은 블랙홀과 중성자별과 같은 초고밀도 물체에 매우 가깝게 접근할 때만 커진다.

슈바르츠실트 해는 $r=0$과 $r=r_s$에서 특이점을 갖는 것으로 보인다. $r = r_s$에서의 특이점은 좌표 특이점의 예시이다. 그러나 $r=0$의 경우는 중력 특이점으로 시공간 자체가 더이상 잘 정의되지 않는다.

모든 $r>0$에 유효한 것으로 간주되는 슈바르츠실트 해는 '''슈바르츠실트 블랙홀'''이라고 한다. $r < r_s$의 경우 슈바르츠실트 반경 좌표 $r$은 시간과 같게되고, 시간 좌표 $t$는 공간과 같게된다. $r=r_s$ 표면은 블랙홀의 ''사건의 지평선''이라고 불리는 것을 구분한다. 이는 더 이상 중력장을 벗어날 수 없는 지점을 나타낸다. 반경 $R$이 슈바르츠실트 반경보다 작거나 같아지는 모든 물리적 객체는 중력 붕괴를 겪었고 블랙홀이 되었다.

2. 1. 슈바르츠실트 좌표

슈바르츠실트 계량은 구면 대칭 로렌츠 계량으로, 빈 공간에서 아인슈타인의 장 방정식의 해이다. 이는 중력체를 제외한 ''바깥''에서만 유효하며, 반지름

R

인 구형 물체의 경우

r > R

에서 유효하다. 중력체 내부와 외부 모두를 설명하기 위해 슈바르츠실트 해는

r = R

에서 내부 슈바르츠실트 계량과 같은 적절한 내부 해와 일치해야 한다.^[4]

슈바르츠실트 좌표

(t, r, \theta, \phi)

에서 슈바르츠실트 계량 (또는 그에 상응하는, 고유 시간에 대한 선 요소)은 다음과 같다.

{d s}^{2} = c^2 \,{d \tau}^{2} = \left (1 - \frac{r_\mathrm{s}}{r} \right) c^2 \,dt^2 - \left(1-\frac{r_\mathrm{s}}{r}\right)^{-1} \,dr^2 - r^2 {d \Omega}^{2},

여기서

{d \Omega}^{2} = \left(d\theta^2 + \sin^2\theta \, d\phi^2\right)

는 2차원 구에 대한 계량이다. 또한,

$d\tau^2$ 는 시간 유사 곡선에 대해 양수이며, 이 경우 $\tau$ 는 고유 시간이다 (같은 세계선을 따라 움직이는 시계로 측정한 시간으로, 시험 입자와 동일).
$c$ 는 광속이다.
$t$ 는 $r > r_\text{s}$ 에 대해 질량이 큰 물체로부터 무한히 멀리 떨어져 있고 이에 대해 정지해 있는 시계로 측정된 시간 좌표이다.
$r$ 는 $r > r_\text{s}$ 에 대해 질량이 큰 물체 주위에 중심이 있는 구의 둘레를 2로 나눈 값으로 측정된 반경 좌표이다.
$\Omega$ 는 2차원 구 $S^2$ 의 한 점이다.
$\theta$ 는 임의로 "z"축을 선택한 후 정의되는 $\Omega$ 의 위도이다 (북쪽으로부터의 각도, 라디안 단위)
$\phi$ 는 선택된 "z"축 주위의 $\Omega$ 의 경도이다 (또한 라디안 단위)
$r_\text{s}$ 는 질량이 큰 물체의 슈바르츠실트 반지름이며, 질량 $M$ 과 $r_\text{s} = {2GM}/{c^2}$ 로 관련된 척도 인자이며, 여기서 $G$ 는 중력 상수이다.^[5]

반경 좌표는 "방사형으로 움직이는 측지선 시계에 대해 동시에 발생하는 두 사건 사이의 고유 거리, 두 사건이 동일한 방사형 좌표선에 놓여 있음"으로 물리적 중요성을 갖는다.^[7]

슈바르츠실트 해는 점 입자 주위의 중력장에 해당하는 고전적인 뉴턴 중력 이론과 유사하며, 지구 표면에서도 뉴턴 중력에 대한 수정은 10억 분의 1에 불과하다.^[8] 지구의 슈바르츠실트 반지름은 약 8.9mm이고,^[6] 태양의 슈바르츠실트 반지름은 약 3.0km이다. 이 비율은 블랙홀과 중성자별과 같은 초고밀도 물체에 매우 가깝게 접근할 때만 커진다.

2. 2. 주요 특징

슈바르츠실트 해는 $r=0$과 $r=r_s$에서 특이점을 갖는 것으로 보인다.^[20] 일부 계량 성분은 이러한 반경에서 "발산"(0으로 나누거나 무한대로 곱함)한다. 슈바르츠실트 계량이 중력체를 포함하는 물체의 반경 $R$보다 큰 반경에 대해서만 유효할 것으로 예상되므로, $R > r_s$인 한 문제가 없다. 일반적인 별과 행성의 경우 이는 항상 그렇다. 예를 들어 태양의 반경은 약 700,000 km인 반면, 슈바르츠실트 반경은 단 3 km이다.

$r = r_s$에서의 특이점은 슈바르츠실트 좌표를 두 개의 분리된 패치로 나눈다.^[20] $r > r_s$인 '외부 슈바르츠실트 해'는 별과 행성의 중력장과 관련된 것이다. $r = 0$의 특이점을 포함하는 $0 \le r < r_s$인 '내부 슈바르츠실트 해'는 $r = r_s$의 특이점에 의해 외부 패치와 완전히 분리된다. 따라서 슈바르츠실트 좌표는 두 패치 사이에 물리적 연결을 제공하지 않으며, 이는 별도의 해로 볼 수 있다. 그러나 $r = r_s$에서의 특이점은 착각이다. 이는 소위 ''좌표 특이점''의 예이다. 이름에서 알 수 있듯이 특이점은 잘못된 좌표 또는 좌표 조건의 선택에서 발생한다. 다른 좌표계(예: 르메트르 좌표, 에딩턴-퓌켈슈타인 좌표, 크러스컬-세케레스 좌표, 노비코프 좌표 또는 굴스트란트-페인르베 좌표)로 변경하면 계량은 $r = r_s$에서 규칙적이 되고 외부 패치를 $r$의 값이 $r_s$보다 작은 값으로 확장할 수 있다. 그런 다음 다른 좌표 변환을 사용하여 확장된 외부 패치를 내부 패치와 연결할 수 있다.^[20]

그러나 $r = 0$의 경우는 다르다. 모든 $r$에 대해 해가 유효해야 한다고 요구하면, 원점에서 실제 물리적 특이점 또는 ''중력 특이점''에 직면하게 된다. 이것이 진정한 특이점임을 확인하려면 좌표 선택에 관계없이 일정한 양을 살펴봐야 한다. 그러한 중요한 양 중 하나는 크레취만 불변량이며, 다음과 같이 주어진다.

:$R^{\alpha\beta\gamma\delta} R_{\alpha\beta\gamma\delta} = \frac{12 r_\mathrm{s}^2}{r^6} = \frac{48 G^2 M^2}{c^4 r^6} \,.$

$r = 0$에서 곡률이 무한대가 되어 특이점의 존재를 나타낸다. 이 시점에서 계량은 매끄러운 방식으로 확장될 수 없으며 (크레취만 불변량은 계량의 2차 도함수를 포함), 시공간 자체가 더 이상 잘 정의되지 않는다.

모든 $r > 0$에 유효한 것으로 간주되는 슈바르츠실트 해는 '''슈바르츠실트 블랙홀'''이라고 한다. 이는 아인슈타인 방정식의 완벽하게 유효한 해이지만 (다른 블랙홀과 마찬가지로) 다소 기괴한 속성을 가지고 있다. $r < r_s$의 경우 슈바르츠실트 반경 좌표 $r$은 시간과 같게 되고, 시간 좌표 $t$는 공간과 같게 된다.^[22] 일정한 $r$에서의 곡선은 더 이상 입자 또는 관찰자의 가능한 세계선이 아니며, 그곳에 유지하기 위해 힘을 가하더라도 마찬가지이다. 이는 시공간이 너무 많이 휘어져서 원인과 결과의 방향 (입자의 미래 광원뿔)이 특이점을 가리키기 때문에 발생한다. $r = r_s$ 표면은 블랙홀의 ''사건의 지평선''이라고 불리는 것을 구분한다. 이는 더 이상 중력장을 벗어날 수 없는 지점을 나타낸다. 반경 $R$이 슈바르츠실트 반경보다 작거나 같아지는 모든 물리적 객체는 중력 붕괴를 겪었고 블랙홀이 되었다.

3. 성질

리치 곡률 스칼라와 리치 곡률 텐서는 모두 0이다. 리만 곡률 텐서의 0이 아닌 성분은 다음과 같다.^[25]

: $-R^{t}{}_{rtr}=2R^{\theta}{}_{r\theta r}=2R^{\phi}{}_{r\phi r}=\frac{r_\text{s}}{r^2(r_\text{s}-r)},$

: $2R^{t}{}_{\theta t\theta}=2R^{r}{}_{\theta r\theta}=-R^{\phi}{}_{\theta\phi\theta}=-\frac{r_\text{s}}{r},$

: $2R^{t}{}_{\phi t\phi}=2R^{r}{}_{\phi r\phi}=-R^{\theta}{}_{\phi\theta\phi}=-\frac{r_\text{s} \sin^2(\theta)}{r},$

: $R^{r}{}_{trt}=-2R^{\theta}{}_{t\theta t}=-2R^{\phi}{}_{t\phi t}= c^2 \frac{r_\text{s} (r_\text{s} - r)}{r^4},$

여기에서 $R^\gamma{}_{\alpha\gamma\beta}=0$ 임을 알 수 있다.

이 공식 중 6개는 Carroll의 식 5.13에 해당하며^[26], $R^\alpha{}_{\beta\gamma\delta}=g^{\alpha\kappa}g_{\beta\lambda}R^\lambda{}_{\kappa\delta\gamma}$ 에 의해 다른 6개를 유추할 수 있다.

리만 텐서의 다른 대칭에 의해 얻을 수 있는 성분은 표시되지 않는다.

이 양들의 물리적 의미를 이해하려면 곡률 텐서를 정규 직교 기저로 표현하는 것이 유용하다. 기하 단위에서 관찰자의 정규 직교 기저에서 0이 아닌 성분은 다음과 같다.^[25]

: $R^{\hat{r}}{}_{\hat{t}\hat{r}\hat{t}}= -R^{\hat{\theta}}{}_{\hat{\phi}\hat{\theta}\hat{\phi}} = -\frac{r_\text{s}}{r^3},$

: $R^{\hat{\theta}}{}_{\hat{t}\hat{\theta}\hat{t}}= R^{\hat{\phi}}{}_{\hat{t}\hat{\phi}\hat{t}} = -R^{\hat{r}}{}_{\hat{\theta}\hat{r}\hat{\theta}} = -R^{\hat{r}}{}_{\hat{\phi}\hat{r}\hat{\phi}} = \frac{r_\text{s}}{2r^3}.$

다시 말해, 리만 텐서의 대칭에 의해 얻을 수 있는 성분은 표시되지 않는다. 이러한 결과는 모든 로렌츠 부스트에 불변하므로, 정지하지 않은 관찰자에게도 성분이 변하지 않는다. 측지선 이탈 방정식은 $\xi^{\hat{j}}$ 로 분리된 두 관찰자 사이의 조석 가속도가 $D^2 \xi^{\hat{j}}/D\tau^2 = -R^{\hat{j}}{}_{\hat{t}\hat{k}\hat{t}} \xi^{\hat{k}}$ 임을 보여주므로, 길이 $L$ 인 물체는 방사 방향으로 $(r_\text{s}/r^3)c^2 L$ 의 겉보기 가속도로 늘어나고 수직 방향으로는 $-(r_\text{s}/(2r^3)) c^2 L$ 로 압착된다.

3. 1. 질량과 열역학

슈바르츠실트 계량의 ADM 질량

M

은 다음과 같다.^[47]

:

M=\frac{(d-2)\operatorname{vol}(S^{d-2})r_0^{d-3}}{16\pi G}

여기서

G

는

d

차원 중력 상수이며,

:

\operatorname{vol}(S^{d-2})=\frac{(d-1)\pi^{(d-1)/2}}{\Gamma((d+1)/2)}

는

d-2

차원 초구의 부피이다. 예를 들어, 4차원의 경우

:

M=r_0/2G

이다.

윅 회전을 통해 계산하면, 임의의 차원에서 슈바르츠실트 블랙홀의 온도는 다음과 같다.

:

T=\frac{\hbar c}{4\pi k_{\text{B}}r_0}

다시 말해, 슈바르츠실트 블랙홀은 이 온도의 호킹 복사를 방출한다.

사건 지평선의 넓이가

:

A=\operatorname{vol}(S^{d-2})r_0^{d-2}

이므로, 슈바르츠실트 해의 엔트로피는

:

S=A/4G

이다.

3. 2. 인과 구조

슈바르츠실트 계량은 점근적으로 평탄하여, 원점에서 매우 멀리 떨어진 곳에서는 민코프스키 공간에 근접한다. 슈바르츠실트 계량은

r=r_s

에서 사건 지평선을 가지며, 이를 슈바르츠실트 반지름이라고 한다. 이 지점에서 계량 텐서가 발산하는 것처럼 보이지만, 이는 좌표 특이점에 불과하며, 다른 좌표계를 사용해 지평선 내부가 존재함을 보일 수 있다.^[20]

슈바르츠실트 해는

r=0

과

r=r_s

에서 특이점을 갖는 것으로 보인다.

r=r_s

에서의 특이점은 슈바르츠실트 좌표를 두 개의 분리된 패치로 나누는데,

r>r_s

인 외부 슈바르츠실트 해는 별과 행성의 중력장과 관련이 있다.

0\le r 인 내부 슈바르츠실트 해는 r=0 의 특이점을 포함하며 외부 패치와 완전히 분리되어, 두 패치 사이에 물리적 연결은 없다.

^[44] 그러나

r=r_s

에서의 특이점은 좌표 선택으로 인한 착각으로, 르메트르 좌표, 에딩턴-퓌켈슈타인 좌표 등 다른 좌표계로 변경하면 계량은

r=r_s

에서 규칙적이 되고 외부 패치를

r 값으로 확장하여 내부 패치와 연결할 수 있다.

^[44]

반면

r=0

에서는 크레취만 불변량이

:

R^{\alpha\beta\gamma\delta} R_{\alpha\beta\gamma\delta} = \frac{12 r_\mathrm{s}^2}{r^6} = \frac{48 G^2 M^2}{c^4 r^6} \,.

와 같이 주어지며, 곡률이 무한대가 되어 중력 특이점의 존재를 나타낸다. 이 시점에서 계량과 시공간 자체는 더 이상 잘 정의되지 않는다.^[21]

r>0

에 유효한 슈바르츠실트 해는 슈바르츠실트 블랙홀이라고 불리는 아인슈타인 장 방정식의 해이다.

r 의 경우 슈바르츠실트 반경 좌표 r 은 시간과 같게 되고, 시간 좌표 t 는 공간과 같게 된다.

^[22] 일정한

r

에서의 곡선은 시공간이 너무 많이 휘어져 원인과 결과의 방향이 특이점을 가리키기 때문에, 입자 또는 관찰자의 가능한 세계선이 될 수 없다.

r=r_s

표면은 사건의 지평선으로, 중력장을 벗어날 수 없는 지점을 나타낸다.^[45]

3. 3. 대칭

슈바르츠실트 계량은

d-1

차원 공간의 회전에 대하여 불변이며, 시간 변화에 대하여도 불변인

\operatorname O(d-1) \times \mathbb R

대칭을 갖는다. 이는 총

(d-1)(d-2)/2+1

개의 킬링 벡터장에 해당한다.

버코프의 정리에 의하여, 진공이면서 구면 대칭을 갖는 아인슈타인 방정식의 해는 슈바르츠실트 계량 밖에 없다. 슈바르츠실트 계량의 등거리 변환군은

\mathrm{O}(3)

는 3차원 직교군의 회전 및 반사,

\mathbb R

은 시간 이동,

\{\pm 1\}

은 시간 반전에 의해 생성된 군을 나타내는 이다.

이는 10차원 푸앵카레 군의 부분군으로, 시간축(별의 궤적)을 자기 자신으로 가져간다. 공간 이동(3차원)과 부스트(3차원)는 생략되며, 시간 이동(1차원)과 회전(3차원)은 유지된다. 따라서 4차원을 갖는다. 푸앵카레 군과 마찬가지로, 항등 성분, 시간 반전 성분, 공간 반전 성분, 시간 반전 및 공간 반전 성분을 모두 포함하는 성분 등 네 개의 연결 성분으로 구성된다.

4. 일반화

슈바르츠실트 블랙홀에 전하를 띠게 한 해는 라이스너-노르드스트룀 계량이다. 현실에서의 중력 붕괴 현상으로 형성되는 블랙홀은 회전하는 블랙홀이 될 것으로 여겨진다. 회전하는 블랙홀에 대한 해는 커 계량이, 거기에 더해 전하를 띠는 경우에는 커-뉴먼 계량이 유일한 해이다.

4. 1. 회전하는 블랙홀

현실에서의 중력 붕괴 현상으로 형성되는 블랙홀은 회전하는 블랙홀이 될 것으로 여겨진다. 회전하는 블랙홀에 대한 해는 커 계량이, 거기에 더해 전하를 띠는 경우에는 커-뉴먼 계량이 유일한 해이다. 슈바르츠실트 블랙홀에 전하를 띠게 한 해는 라이스너-노르드스트룀 계량이다.

4. 2. 전하를 띤 블랙홀

라이스너-노르드스트룀 계량은 슈바르츠실트 블랙홀에 전하를 띠게 한 해이다. 현실에서의 중력 붕괴 현상으로 형성되는 블랙홀은 회전하는 블랙홀이 될 것으로 여겨진다. 회전하는 블랙홀에 대한 해는 커 계량이, 거기에 더해 전하를 띠는 경우에는 커-뉴먼 계량이 유일한 해이다.

4. 3. 우주 상수

슈바르츠실트 블랙홀에 전하를 띠게 한 해는 라이스너-노르드스트룀 계량이다. 현실에서 중력 붕괴로 형성되는 블랙홀은 회전하는 블랙홀이 될 것으로 예상되며, 이에 대한 해는 커 계량이다. 전하를 띠는 회전하는 블랙홀의 경우 커-뉴먼 계량이 유일한 해이다.

양의 우주 상수

\Lambda=(d-1)(d-2)R^{-2}/2

를 가진,

d>3

차원의 더 시터르 공간에서, 구형 대칭의 정적 비대전 계량은 '''슈바르츠실트-더 시터르 계량'''(Schwarzschild-de Sitter計量, Schwarzschild–de Sitter metric}})이라고 하며, 다음과 같다.^[48]

:

\mathrm ds^2=-\left(1-(r_0/r)^{d-3}-r^2/R^2\right)\mathrm dt^2+\left(1-(r_0/r)^{d-3}-r^2/R^2\right)^{-1}dr^2+r^2\,\mathrm d\Omega_{d-2}^2

슈바르츠실트-더 시터르 계량의 질량은 다음과 같다. (이는 더 시터르 공간의 질량이 0이라고 가정한 것이다.)

:

M=\frac{(d-2)\operatorname{vol}(S^{d-2})r_0^{d-3

^영어{16\pi G}

슈바르츠실트-더 시터르 계량은

1=(r_0/r)^{d-3}+r^2/R^2

인 곳에서 킬링 지평선(킬링 벡터

\partial/\partial t

가 영벡터가 되는 점)을 가진다. 이 식은 일반적으로 두 개의 해를 가지는데, 안쪽은 블랙홀, 바깥쪽은 더 시터르 공간의 우주론적 지평선(cosmological horizon^영어)이다. 두 지평선은 일반적으로 서로 다른 온도를 가지며, 따라서 서로 다른 온도의 호킹 복사를 방출한다.^[49]^[50]

음의 우주 상수

\Lambda=-(d-1)(d-2)R^{-2}/2

를 가진,

d>2

차원의 반 더 시터르 공간에서, 구형 대칭의 정적 비대전 계량은 '''슈바르츠실트-반 더 시터르 계량'''(Schwarzschild-反de Sitter計量, Schwarzschild–anti-de Sitter metric}})이라고 한다.^[47] 이 경우 3차원에서도 블랙홀이 존재하는데, 이를 BTZ 블랙홀이라고 한다.

:

ds^2=-\left(1-(r_0/r)^{d-3}+r^2/R^2\right)dt^2+\left(1-(r_0/r)^{d-3}+r^2/R^2\right)^{-1}dr^2+r^2d\Omega_{d-2}^2

슈바르츠실트-반 더 시터르 계량의 질량은 다음과 같다. (이는 반 더 시터르 공간의 질량이 0이라고 가정한 것이다.)

:

M=\frac{(d-2)\operatorname{vol}(S^{d-2})r_0^{d-3

^영어{16\pi G}

반 더 시터르 공간의 온도를 질량에 따른 함수

T(M)

라고 하면, 이 함수는 어떤

M_0

에 대하여

M\le M_0

인 경우 감소,

M\ge M_0

인 경우 증가한다. 즉, 같은 온도를 가지지만 서로 다른 에너지를 가진 두 블랙홀이 존재하며, 블랙홀의 최저 온도

T_\text{min}

가 존재한다. 이 온도에서 블랙홀은 1차 상전이를 겪는데, 이를 '''호킹-페이지 전이'''(Hawking–Page transition^영어)라고 하며, 스티븐 호킹과 돈 페이지(Don Page^영어)가 발견하였다.^[51] 이는 AdS/CFT 대응성을 통해, 대응하는 등각 장론의 상전이로 해석할 수 있다.

이 계량은

1-(r_0/r)^{d-3}+r^2/R^2=0

이 되는

r

에서 사건 지평선을 갖는다.

5. 좌표계

슈바르츠실트 해는 위에 사용된 슈바르츠실트 좌표 외에도 다양한 좌표 선택으로 표현할 수 있다. 서로 다른 선택은 해의 서로 다른 특징을 강조하는 경향이 있다. 아래 표는 몇 가지 인기 있는 선택 사항을 보여준다.^[23]

대안 좌표
좌표	선 요소	참고	특징
에딩턴-핑켈슈타인 좌표(내부로 들어오는)	$\left(1-\frac{r_\mathrm{s}}{r} \right)\, dv^2 - 2 \,dv \,dr - r^2 \,g_\Omega$		미래 지평선에서 정규적 과거 지평선은 에 위치
에딩턴-핑켈슈타인 좌표(외부로 나가는)	$\left(1-\frac{r_\mathrm{s}}{r} \right)\, du^2 + 2 \,du \,dr - r^2 g_\Omega$		과거 지평선에서 정규적 과거 지평선을 넘어 확장 미래 지평선은 에 위치
굴스트란트-페인레베 좌표	$\left(1-\frac{r_\mathrm{s}}{r} \right)\,dT^2 \pm 2\sqrt\frac{r_\mathrm{s}}{r} \,dT \,dr - dr^2-r^2\,g_\Omega$		과거 및 미래 지평선에서 정규적
등방 좌표	$\frac{\left(1-\frac{r_\mathrm{s}}{4R}\right)^2}{\left(1+\frac{r_\mathrm{s}}{4R}\right)^2}\,{dt}^2 - \left(1+\frac{r_\mathrm{s}}{4R}\right)^4\,\left(dx^2+dy^2+dz^2\right)$	$R = \sqrt{ x^2 + y^2 + z^2 }$ ^[24]	사건 지평선 외부에서만 유효: $R > r_\text{s}/4$	일정 시간 슬라이스에서 등방 광원뿔
크러스컬-세케레스 좌표	$\frac{4r_\mathrm{s}^3}{r}e^{-\frac{r}{r_\mathrm{s}}}\,\left(dT^2 - dR^2\right)- r^2 \,g_\Omega$	$T^2 - R^2 = \left(1-\frac{r}{r_\mathrm{s}}\right)e^\frac{r}{r_\mathrm{s}}$	지평선에서 정규적; 전체 시공간으로 최대한 확장
르메트르 좌표	$dT^{2} - \frac{r_\mathrm{s}}{r}\, dR^2 - r^2\,g_\Omega$	$r = \left(\tfrac32(R\pm T)\right)^\frac23 r_\mathrm{s}^\frac13$	과거 또는 미래 지평선에서 정규적
조화 좌표	$\frac{\rho-r_\mathrm{s}/2}{\rho+r_\mathrm{s}/2} dt^2 - \frac{\rho+r_\mathrm{s}/2}{\rho-r_\mathrm{s}/2} d\rho^2 -(\rho+r_\mathrm{s}/2)^2 g_\Omega$	$\rho=r-r_\mathrm{s}/2$

위 표에서 간결성을 위해 몇 가지 약어가 도입되었다. 빛의 속도는 자연 단위로 1로 설정되었다. 다음 표기법

: $g_\Omega= d\theta^2+\sin^2\theta \,d\varphi^2$

는 단위 반지름 2차원 구의 메트릭에 사용된다. 또한, 각 항목에서 및 는 특정 좌표에 대한 반경 및 시간 좌표의 대안적 선택을 나타낸다. 참고로, 또는 는 항목마다 다를 수 있다.

크러스컬-세케레스 좌표는 벨린스키-자하로프 변환을 적용할 수 있는 형태를 가지고 있다. 이는 슈바르츠실트 블랙홀이 중력 솔리톤의 한 형태임을 의미한다.

5. 1. 에딩턴-핑켈슈타인 좌표

슈바르츠실트 해는 슈바르츠실트 좌표 외에 다양한 좌표계로 표현될 수 있으며, 각 좌표계는 해의 서로 다른 특징을 강조한다.^[23]

(내부로 들어오는) 에딩턴-핑켈슈타인 좌표는 다음과 같은 선 요소를 갖는다.

:

\left(1-\frac{r_\mathrm{s}}{r} \right)\, dv^2 - 2 \,dv \,dr - r^2 \,g_\Omega

이 좌표는 미래 지평선에서 정규적이며, 과거 지평선은 에 위치한다.

(외부로 나가는) 에딩턴-핑켈슈타인 좌표는 다음과 같은 선 요소를 갖는다.

:

\left(1-\frac{r_\mathrm{s}}{r} \right)\, du^2 + 2 \,du \,dr - r^2 g_\Omega

이 좌표는 과거 지평선에서 정규적이며, 미래 지평선은 에 위치한다.

5. 2. 크루스칼-세케레스 좌표

슈바르츠실트 해는 슈바르츠실트 좌표 외에도 다양한 좌표계로 표현될 수 있으며, 각 좌표계는 해의 서로 다른 특징을 강조한다.^[23] 그 중 크러스컬-세케레스 좌표는 다음과 같이 표현된다.

:

\frac{4r_\mathrm{s}^3}{r}e^{-\frac{r}{r_\mathrm{s}}}\,\left(dT^2 - dR^2\right)- r^2 \,g_\Omega

여기서

T^2 - R^2 = \left(1-\frac{r}{r_\mathrm{s}}\right)e^\frac{r}{r_\mathrm{s}}

이다. 이 좌표계는 지평선에서 정규적이며, 전체 시공간으로 최대한 확장된다는 특징을 갖는다. 또한 크루스칼-세케레스 좌표는 벨린스키-자하로프 변환을 적용할 수 있는 형태를 가지는데, 이는 슈바르츠실트 블랙홀이 중력 솔리톤의 한 형태임을 의미한다.

다른 좌표계로는 에딩턴-핑켈슈타인 좌표, 굴스트란트-페인레베 좌표, 등방 좌표, 르메트르 좌표 등이 있다.

5. 3. 르메트르 좌표

슈바르츠실트 해는 슈바르츠실트 좌표 외에도 다양한 좌표 선택으로 표현할 수 있으며, 서로 다른 선택은 해의 서로 다른 특징을 강조한다.^[23] 르메트르 좌표는 다음과 같다.

:

dT^{2} - \frac{r_\mathrm{s}}{r}\, dR^2 - r^2\,g_\Omega

여기서

r = \left(\tfrac32(R\pm T)\right)^\frac23 r_\mathrm{s}^\frac13

이고,

g_\Omega= d\theta^2+\sin^2\theta \,d\varphi^2

는 단위 반지름 2차원 구의 메트릭이다. 르메트르 좌표는 과거 또는 미래 지평선에서 정규적이다.^[23]

5. 4. 등방 좌표

슈바르츠실트 해는 슈바르츠실트 좌표 외에도 다양한 좌표 선택으로 표현할 수 있으며, 서로 다른 선택은 해의 서로 다른 특징을 강조한다.^[23] 등방 좌표에서 슈바르츠실트 계량은 다음과 같이 표현된다.

:

\frac{\left(1-\frac{r_\mathrm{s}}{4R}\right)^2}{\left(1+\frac{r_\mathrm{s}}{4R}\right)^2}\,{dt}^2 - \left(1+\frac{r_\mathrm{s}}{4R}\right)^4\,\left(dx^2+dy^2+dz^2\right)

여기서

R = \sqrt{ x^2 + y^2 + z^2 }

이다.^[24] 이 좌표계는 사건 지평선 외부(

R > r_\text{s}/4

)에서만 유효하며, 일정 시간 슬라이스에서 등방 광원뿔을 가진다.

6. 궤도 운동

뉴턴 (왼쪽) 시공간과 슈바르츠실트 (오른쪽) 시공간에서 시험 입자의 궤도 비교; 오른쪽의 근점 세차 운동에 주목하십시오.

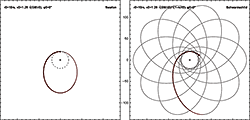
슈바르츠실트 계량에서 궤도를 도는 입자는 ''r'' > 3''r''_s인 안정적인 원궤도를 가질 수 있다. ''r''이 1.5''r''_s와 3''r''_s 사이인 원형 궤도는 불안정하며, ''r'' < 1.5''r''_s인 원형 궤도는 존재하지 않는다. 최소 반경 1.5''r''_s의 원형 궤도는 빛의 속도에 접근하는 궤도 속도에 해당한다. 입자가 ''r''_s와 1.5''r''_s 사이에서 ''r''의 일정한 값을 가질 수 있지만, 이는 어떤 힘이 작용하여 그 위치에 유지하는 경우에만 가능하다.

수성과 같은 비원형 궤도는 뉴턴 중력에서 예상되는 것보다 작은 반경에서 더 오래 머문다. 이것은 입자가 사건의 지평선을 통과하여 영원히 그 안에 머무는 더 극적인 경우의 덜 극단적인 버전으로 볼 수 있다. 수성의 경우와 사건의 지평선을 지나 떨어지는 물체의 경우 사이에는 칼날 궤도와 같은 이국적인 가능성이 있으며, 이 궤도에서는 인공위성이 임의로 많은 수의 거의 원형 궤도를 실행하도록 만든 다음 다시 바깥쪽으로 날아갈 수 있다.

6. 1. 안정된 원궤도

슈바르츠실트 계량에서 궤도를 도는 입자는 ''r'' > 3''r''_s인 안정적인 원형 궤도를 가질 수 있다. ''r''이 1.5''r''_s와 3''r''_s 사이인 원형 궤도는 불안정하며, ''r'' < 1.5''r''_s인 원형 궤도는 존재하지 않는다. 최소 반경 1.5''r''_s의 원형 궤도는 빛의 속도에 접근하는 궤도 속도에 해당한다. 입자가 ''r''_s와 1.5''r''_s 사이에서 ''r''의 일정한 값을 가질 수 있지만, 이는 어떤 힘이 작용하여 그 위치에 유지하는 경우에만 가능한다.

수성과 같은 비원형 궤도는 뉴턴 중력에서 예상되는 것보다 작은 반경에서 더 오래 머문다. 이것은 입자가 사건의 지평선을 통과하여 영원히 그 안에 머무는 더 극적인 경우의 덜 극단적인 버전으로 볼 수 있다. 수성의 경우와 사건의 지평선을 지나 떨어지는 물체의 경우 사이에는 칼날 궤도와 같은 이국적인 가능성이 있으며, 이 궤도에서는 인공위성이 임의로 많은 수의 거의 원형 궤도를 실행하도록 만든 다음 다시 바깥쪽으로 날아갈 수 있다.

6. 2. 불안정한 원궤도

슈바르츠실트 계량 아래에서 입자는 r > 3r_s 인 경우 안정적인 원궤도를 그릴 수 있다. 3r_s/2 < r < 3r_s 사이의 경우 원궤도는 불안정해지며, r < 3r_s/2 의 경우 원궤도는 존재하지 않는다. 이 최소 반경 3r_s/2 에서의 원궤도는 궤도 속도가 광속이 되는 궤도에 해당한다. r_s < r < 3r_s/2 의 경우에도 원을 그리게 할 수 있지만, 어떤 힘을 가해야 한다.

수성과 같은 비원형 궤도에서는 뉴턴 역학에서 예측되는 것보다 긴 시간 동안 반경이 작은 부분에 머문다. 이 사실을 입자가 사건의 지평선을 넘어 영원히 나오지 못하는 경우의 덜 극단적인 예라고 생각할 수도 있다. 수성의 경우와 사건의 지평선에 떨어지는 경우 사이의 중간 예에는, 예를 들어, 임의의 횟수만큼 거의 원형 궤도를 그린 후 바깥쪽으로 돌아오는 "나이프 에지" 궤도와 같은 직관적이지 않은 예가 존재한다.

6. 3. 최소 원궤도 반지름

슈바르츠실트 계량 아래에서 입자는 r > 3r_s 인 경우 안정적인 원궤도를 그릴 수 있다. 3r_s/2 < r < 3r_s 사이의 경우 원궤도는 불안정해지며, r < 3r_s/2 의 경우 원궤도는 존재하지 않는다. 이 최소 반경 3r_s/2 에서의 원궤도는 궤도 속도가 광속이 되는 궤도에 해당한다. r_s < r < 3r_s/2 의 경우에도 원을 그리게 할 수 있지만, 어떤 힘을 가해야 한다.

수성과 같은 비원형 궤도에서는 뉴턴 중력에서 예측되는 것보다 긴 시간 동안 반경이 작은 부분에 머문다. 이 사실을 입자가 사건의 지평선을 넘어 영원히 나오지 못하는 경우의 덜 극단적인 예라고 생각할 수도 있다. 수성의 경우와 사건의 지평선에 떨어지는 경우 사이의 중간 예에는, 예를 들어, 임의의 횟수만큼 거의 원형 궤도를 그린 후 바깥쪽으로 돌아오는 "나이프 에지" 궤도와 같은 직관적이지 않은 예가 존재한다.

6. 4. 수성의 근일점 이동

슈바르츠실트 계량 아래에서 입자는 인 안정적인 원궤도를 그릴 수 있다. 사이의 경우 원궤도는 불안정해지며, 의 경우 원궤도는 존재하지 않는다. 이 최소 반경 에서의 원궤도는 궤도 속도가 광속이 되는 궤도에 해당한다. 의 경우에도 원을 그리게 할 수 있지만, 어떤 힘을 가해야 한다.

수성과 같은 비원형 궤도에서는 뉴턴 역학에서 예측되는 것보다 긴 시간 동안 반경이 작은 부분에 머문다. 이 사실을 입자가 사건의 지평선을 넘어 영원히 나오지 못하는 경우의 덜 극단적인 예라고 생각할 수도 있다. 수성의 경우와 사건의 지평선에 떨어지는 경우 사이의 중간 예에는, 예를 들어, 임의의 횟수만큼 거의 원형 궤도를 그린 후 바깥쪽으로 돌아오는 "나이프 에지" 궤도와 같은 직관적이지 않은 예가 존재한다.

7. 역사

카를 슈바르츠실트는 일반 상대성 이론이 발표된 직후인 1916년 1월에 이 해를 발표했다.^[9]^[52] 제1차 세계 대전 당시 슈바르츠실트는 독일군에 복무하면서 천포창으로 추정되는 질병으로 사망했다.^[10] 그는 출병 전에 일반 상대성 이론을 접한 뒤, 전쟁터에서 계산에 힘써 이 해를 도출해냈고, 그 연구 결과를 알베르트 아인슈타인에게 보냈다.^[52] 슈바르츠실트 해는 민코프스키 시공간을 제외한 최초의 정확한 해였다.^[9]

슈바르츠실트는 자신이 발견한 해에 대하여 다음과 같이 평했다.

}}

요하네스 드로스테는 1916년에 슈바르츠실트와 동일한 해를 더 간단하고 직접적인 유도를 통해 독립적으로 만들어냈다.^[11]^[12]

일반 상대성 이론 초창기에는 슈바르츠실트 해와 기타 아인슈타인 장 방정식 해에서 발견된 특이점의 본질에 대해 많은 혼란이 있었다. 슈바르츠실트의 원본 논문에서 그는 현재 사건의 지평선이라고 부르는 것을 자신의 좌표계의 원점에 두었다.^[35] 이후 다비트 힐베르트가 특이점 구조에 대한 보다 완벽한 분석을 제공했다.^[13]

1921년 폴 팽르베와 1922년 알바르 굴스트란드는 굴스트란드-팽르베 좌표를 독립적으로 만들어냈는데, 이들은 에 특이점이 없었다. 1924년 아서 에딩턴은 에딩턴-핀켈슈타인 좌표를 통해 에서의 특이점이 좌표 인공물임을 보여주었다. 1932년 조르주 르메트르는 르메트르 좌표를 통해 에서의 특이점이 물리적이지 않음을 처음으로 인식했다. 1939년 하워드 퍼시 로버트슨은 슈바르츠실트 계량에서 자유 낙하하는 관측자가 유한한 고유 시간 내에 특이점을 통과할 것임을 보여주었다.^[14]

1950년 존 라이턴 싱은 슈바르츠실트 계량의 최대 해석적 확장을 보여주는 논문을 발표했다.^[15] 이와 유사한 결과는 나중에 게오르그 세케레스^[16]와 마르틴 크루스칼^[17]에 의해 독립적으로 재발견되었다. 현재 크루스칼-세케레스 좌표로 알려진 새로운 좌표는 싱의 좌표보다 훨씬 간단했지만, 둘 다 전체 시공간을 커버하는 단일 좌표 집합을 제공했다.

1960년대에 미분 기하학의 관점에서 수학적으로 엄격한 공식화가 이루어지면서, 슈바르츠실트 계량에서 특이점이 사건의 지평선으로 확실하게 식별되었다.^[14]

8. 플람의 쌍곡면

슈바르츠실트 해의 }} 에서의 공간 곡률은 그림과 같이 도식화할 수 있다. 슈바르츠실트 해의 일정 시간・적도면 ()에서의 단면을 생각한다. 이 평면 위를 운동하는 입자의 위치는 나머지 슈바르츠실트 좌표 에 의해 나타낼 수 있다. 여기에 또 하나의 가상의 유클리드 차원 (시공의 일부가 아님)을 추가한 곳을 상상해 보자. 그리고 평면을 방향으로 다음과 같이 움푹 들어간 곡면(플람의 쌍곡면)으로 바꾼다.

:

w = 2 \sqrt{r_\mathrm{s} \left( r - r_\mathrm{s} \right)}.

이 곡면은 그 위에서 측정하는 거리가 슈바르츠실트 계량에 의해 정의된 것과 일치한다는 성질을 갖는다. 왜냐하면, 위의 의 정의에 의해, 다음 식이 성립한다.

:

\mathrm dw^2 + \mathrm dr^2 + r^2 \mathrm d\varphi^2 = -c^2 \mathrm d\tau^2 = \frac{\mathrm dr^2}{1 - \frac{r_\mathrm s}{r}} + r^2 \mathrm d\varphi^2

이 때문에, 플람의 쌍곡면은 슈바르츠실트 계량에서의 공간의 왜곡을 시각화하는 데 편리하다. 그러나, 이것을 중력 우물의 개념과 혼동해서는 안 된다. 통상의 입자는 (질량의 유무에 관계없이) 이 쌍곡면 위에 세계선을 따라갈 수 없다. 왜냐하면, 이 쌍곡면 위의 선분은 모두 공간적이기 때문이다 (이것은 어떤 순간에서의 단면이며, 모든 움직이는 입자는 무한대의 속도를 갖게 된다). 타키온을 가져온다고 해도, "고무막"의 아날로지를 순진하게 적용했을 때 예상되는 궤적을 따르는 것은 아니다. 일례로, 이 움푹 들어간 부분이 아래쪽이 아니라 위쪽으로 그려져 있더라도, 타키온의 궤적은 중심 질량으로 향하도록 굽혀질 뿐 멀어지도록 굽혀지지는 않는다.

플람의 쌍곡면은 다음과 같이 유도할 수 있다. 유클리드 계량 하의 거리를 원통 좌표계 를 사용하여 쓰면 아래와 같이 쓸 수 있다.

:

\mathrm{d}s^2 = \mathrm{d}w^2 + \mathrm{d}r^2 + r^2 \mathrm{d}\phi^2

이 곡면을 라는 함수로 나타낸다고 하면, 유클리드 계량은 다음과 같이 쓸 수 있다.

:

\mathrm{d}s^2 = \left[ 1 + \left(\frac{\mathrm{d}w}{\mathrm{d}r}\right)^2 \right] \mathrm{d}r^2 + r^2\mathrm{d}\phi^2

이것을 어떤 고정 시간 하에서 에서의 적도면 ()에서의 슈바르츠실트 계량에서의 거리

:

\mathrm{d}s^2 = \left(1-\frac{r_{s}}{r} \right)^{-1} \mathrm{d}r^2 + r^2\mathrm{d}\phi^2

과 비교하면 의 적분 표시는 다음과 같이 쓸 수 있다는 것을 알 수 있다.

:

w(r) = \int \frac{\mathrm{d}r}{\sqrt{\frac{r}{r_\mathrm{s}}-1}} = 2 r_{s} \sqrt{\frac{r}{r_\mathrm{s}}- 1} + \mbox{constant}

이 해가 플람의 쌍곡면이다.

참조

_[1] 논문 Image of a spherical black hole with thin accretion disk. https://ui.adsabs.ha[...] 1979-05-01
_[2] 논문 Gravitational lensing in the strong field limit https://link.aps.org[...] 2002-11-22
_[3] 논문 Divergent reflections around the photon sphere of a black hole 2021-07-09
_[4] 서적 Introduction to Black Hole Physics https://archive.org/[...] Oxford
_[5] 문서
_[6] 서적 Science Data Book Oliver & Boyd
_[7] 논문 The Schwarzschild radial coordinate as a measure of proper distance 1978-05-15
_[8] 논문 Examples of Newtonian limits of relativistic spacetimes http://pubman.mpdl.m[...] 1997-01-01
_[9] 논문 Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie https://archive.org/[...]
_[10] 웹사이트 Karl Schwarzschild
_[11] 논문 The field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field http://www.dwc.knaw.[...]
_[12] 서적 Studies in the History of General Relativity Birkhäuser
_[13] 논문 Die Grundlagen der Physik Springer-Verlag
_[14] 서적 The expanding worlds of general relativity Birkhäuser
_[15] 논문 The gravitational field of a particle
_[16] 논문 On the singularities of a Riemannian manifold
_[17] 논문 Maximal extension of Schwarzschild metric
_[18] 논문 Model universes with spherical symmetry 1974-12-01
_[19] 서적 The mathematical theory of black holes Clarendon Press 2009
_[20] 서적 An introduction to general relativity https://archive.org/[...] Cambridge University Press
_[21] arXiv The ''C''⁰-inextendibility of the Schwarzschild spacetime and the spacelike diameter in Lorentzian Geometry
_[22] 서적 Time: A Traveler's Guide. Oxford University Press, Incorporated 1999
_[23] 서적 One Hundred Years of General Relativity: From Genesis and Empirical Foundations to Gravitational Waves, Cosmology and Quantum Gravity https://books.google[...] World Scientific 2017-05-26
_[24] 서적 The Mathematical Theory of Relativity Cambridge University Press
_[25] 서적 Gravitation W. H. Freeman 1973
_[26] 서적 Spacetime and Geometry: An Introduction to General Relativity Addison Wesley 2004
_[27] 문서
_[28] 논문 Examples of Newtonian limits of relativistic spacetimes http://pubman.mpdl.m[...] 1997-01-01
_[29] 서적 Science Data Book Oliver & Boyd
_[30] 서적 Introduction to Black Hole Physics Oxford
_[31] 논문 Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie https://archive.org/[...]
_[32] 웹사이트 Karl Schwarzschild
_[33] 논문 The field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field http://www.dwc.knaw.[...]
_[34] 서적 Studies in the History of General Relativity Birkhäuser
_[35] 서적 Reflections On Relativity http://mathpages.com[...] Lulu.com
_[36] 논문 Die Grundlagen der Physik Springer-Verlag
_[37] 서적 The expanding worlds of general relativity Birkhäuser
_[38] 서적 The expanding worlds of general relativity Birkhäuser
_[39] 논문 The gravitational field of a particle
_[40] 논문 On the singularities of a Riemannian manifold
_[41] 논문 Maximal extension of Schwarzschild metric
_[42] 서적 The expanding worlds of general relativity Birkhäuser
_[43] 서적 The expanding worlds of general relativity Birkhäuser
_[44] 서적 An introduction to general relativity https://books.google[...] Cambridge University Press
_[45] 논문 Black Hole Horizons and How They Begin http://astroreview.c[...] 2012-01-19
_[46] 서적 The Mathematical Theory of Relativity Cambridge University Press
_[47] 논문 Black holes in higher dimensions
_[48] 논문 Les Houches lectures on De Sitter space
_[49] 논문 Cosmological event horizons, thermodynamics, and particle creation
_[50] 논문 Gravitational thermodynamics of Schwarzschild-de Sitter space
_[51] 논문 Thermodynamics of black holes in anti-de Sitter space https://projecteucli[...]
_[52] 논문 Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie http://www.archive.o[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com